
Research and education in this Department deal with modeling, analysis, and control of complicated and large-scaled systems, not necessarily confined to artificial ones, and optimization of their performances together with basic methodologies such as discrete and applied mathematics, dynamical system theory, and statistical physics. The aim of the Department is to bring up scientists or engineers who can cope with various problems encountered in highly organized and informatized modern societies, based on flexible conception, sharp insight, and high competence for searching solutions, resulting from profound attainments in mathematics and mathematical physics and from a general background in computer sciences.

The Department has 3 divisions, each with 2 or 3 sub-divisions, and consists of 7 chairs. 21 graduate students are accepted into the Master's Program annually and 7 into the Doctoral program.
Applied Mathematical Analysis - Developing algorithms from integrable systems †
We carry out research in the areas of contemporary soliton research
and integrable system research, not only regarding the applied analysis of
orthogonal polynomials and special functions that are closely associated
with integrable systems, but also regarding the application of the mathematical
methods developed by integrable system studies to the solution of
various problems hitherto thought to be unrelated to integrable systems
(such as numerical calculation and algorithm development). Our Group is
a pioneer in this research field, and conducts studies into the applied
analysis of integrable systems in the development of algorithms and other
new branches of mathematics from the perspective of computer science.
(Associate Professor: Satoshi TSUJIMOTO)
Discrete Mathematics -Exploring the complexity of discrete mathematics problems and developing algorithms †
Topics in discrete mathematics, such as the graphs and network used
to represent systems, schedules to enhance the efficiency of production,
and the logical analysis of large volumes of data, are closely related to
applications of research results. We explore the complexity of the calculations
used to solve these problems; design logical approximation algorithms;
develop taboo search algorithms, genetic algorithms and other
metaheuristic algorithms; and apply them to solving actual problems.
(
Associate Professor: Kazuya HARAGUCHI)
System Optimization - Optimization is the keyword for solving problems †
We conduct education and research regarding the theory and methodology
of system optimization, which plays an important role as a mathematical
approach that is used to resolve many different kinds of practical
problems. In particular, we develop efficient mathematical optimization
approaches to actual large-scale systems, complex nonlinear systems, and
systems with uncertainty, as well as basic research regarding mathematical
programming.
(Professor: Nobuo YAMASHITA, Associate Professor: Ellen Hidemi FUKUDA, Program-Specific Associate Professor: Hiroyuki SATO, Assistant Professor: Yuya YAMAKAWA)
Control Systems Theory - Mathematical approaches to modeling and control †
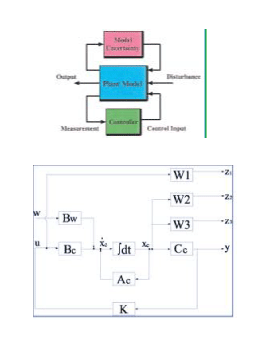
We carry out teaching and research regarding the mathematical
methodologies of modeling, analysis and design of control systems, and
their application with the aim of developing practical and expansive control
theories. Our main research themes are robust control, control systems
with input/output constraints, networked control systems, algebraic
system theory, mathematical optimization in control, stochastic realization
and system identification.
(Associate Professor: Kenji KASHIMA,
Assistant Professor: Kentaro OHKI)
Physical Statistics - The mathematical studies on dynamics of coupled multi-element systems and information processing †
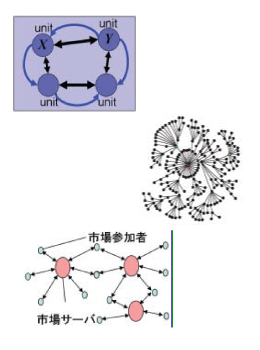
We aim to gain a mathematical and unified understanding of the complex
and diverse phenomena that arise out of the intense mutual interactions
of multiple elements (units) in a system and apply this understanding
to information processing. For example, we will use stochastic process theory,
statistical physics, computer simulations, dynamical system theory,
agent models, and large-scale data processing techniques to analyze information
processing in simple threshold systems, neurons, and their networks;
the structure of the Internet and other complex networks, and the
propagation of information within them; and the dynamical properties of
price change, stock markets and other economic phenomena.
(Professor: Ken UMENO, Junior Associate Professor: Erica UEHARA, Assistant Professor: Atsushi IWASAKI)
Dynamical Systems - Looking into systems through dynamical systems theory †

Our research purpose is that we analyze complicated phenomena such as chaos and bifurcations in various systems appearing in science, engineering and other disciplines using dynamical systems approaches, and apply them to develop novel engineering technologies. For this purpose, we not only use standard approaches but also establish new innovative theories in dynamical systems. Moreover, we utilize numerical approaches such as verifiable computation and large-scale numerical simulation, and study nonintegrability of dynamical systems and differential equations, nonlinear waves in partial differential equations, periodic motions in the n-body problem of classical mechanics and kinetic theory of many-body systems, design of spacecraft transfer trajectories and dynamics and control of flying objects such as quadrocopters.
(Professor: Kazuyuki YAGASAKI, Associate Professor: Mitsuru SHIBAYAMA, Assistant Professor: Yoshiyuki YAMAGUCHI)
Applied Mathematical Modeling Adjunct Unit (in collaboration with Hitachi, Ltd.) - Infusing information systems with intelligence †

To make information systems useful to our day-to-day lives and
industry at large, we need to be able to mathematically model both the
behavior of people and the movements of objects that these systems deal
with. The form of these models ranges from the conceptual to the numerically
precise. We will examine case studies from industry in our research
of modeling technology, including methods of using human knowledge
(structural modeling) and methods using actual data (multivariate analysis).
(Professor: Yoichi NONAKA (Hitachi, Ltd.), Associate Professor: Yoshiyasu TAKAHASHI (Hitachi, Ltd.))
![[AMP] [AMP]](image/amp2.png)